Not: Derin sinir ağlarının öğrenme işleminin ağır bir işlem olmasından dolayı işlem kapasitesi sınırlı cihazlarda ( telefon, tablet vs. ) kasmalar olabilir.
Son zamanlarda yapay zeka ile donatılmış makinelerin bir çok işi başardığına tanıklık etmeye başladık. Özellikle derin sinir ağlarının gelişmesiyle makineler bir hayli güç ve nitelik kazandı. Bu yazımızda biz de yapay zekaya bir şeyler öğretip yeni beceriler kazandıracağız ama bu aşamaya geçmeden önce derin sinir ağlarını biraz yakından tanıyalım.
Derin sinir ağları, makine öğrenmesi algoritmalarının aksine, direkt olarak insan beyninin
bilgisayar ortamında taklit edilmeye (modellenmeye) çalışıldığı yapay zeka algoritmalarıdır.
Bir derin sinir ağını, nöronlar, bu nöronları birbirine bağlayan parametreler ve birtakım işlemler
olarak kısaltabiliriz. Bir derin sinir ağında onlarca , yüzlerce hatta on binlerce nöron
bulunabilir. Bu nöronlar kendi katmanlarından sonraki ve önceki katmanlardaki diğer nöronlarla
bağlıdır.
Modelimize herhangi bir veri girildiğinde bu nöronlar giriş nöronlarından başlamak üzere sıra sıra
birbirlerini dürter ve bu işlem çıkış nöronlarına kadar devam eder. En sonunda çıkış nöronlarındaki
değerler modelimizin tahmin değerleridir.

Yukarıdaki resimde bir sinir ağının görselleştirilmiş halini görebilirsiniz.
Modelimize bir input girerek çıktı alma işlemine İleri Besleme Algoritması, modelimize girilen input ile oluşan çıktıdaki hatayı dağıtarak eğitme işlemine Geriye Besleme Algoritması denmektedir.
Yapay sinir ağlarının çıktı vermesi olayına "İleri Besleme" denmektedir. İleri besleme algoritması kısaca modelimize input girerek çıktı alma işlemidir. İleri besleme algoritmamızı iki aşamaya bölebiliriz;
İnputumuzu giriş katmanımıza girdiğimizde, giriş katmanımızdaki nöronların z değerleri girdiğimiz inputtaki değerleri sırasıyla almaktadır. Artık yeni girişimizi bütün modele yayabiliriz. İlk katmandan sonraki katmanların z değerlerinin atanması işlemine geçilir. Bu kısımda her bir nöronun z değeri, kendinden önceki katmanda bulunan nöronların z değerleri ve bu nöronumuz ile arasındaki ağırlık (w) değeri ile çarpımlarının toplamının aktivasyon fonksiyonuna tabi tutulmuş halini alır. Bu işleme ikinci katmandan başlanıp son katmanda bitirilir.

Yukarıdaki resimde ileri besleme algoritmasını görebilirsiniz.
İleri besleme algoritmasında hangi aktivasyon fonksiyonunu seçeceğimiz konusu probleme göre değişmektedir ancak geriye besleme algoritmasında, ileri besleme algoritmasının türevini kullanacağız. Çoğunlukla sigmoid kullanılıyor olup, biz de bu blog yazısında sigmoid üzerinden ilerleyeceğiz ( sigmoid(x) : 1 / 1+ e -x ).
Yukarıdaki resimde aktivasyon fonksiyonlarını görebilirsiniz.
Hangi derin sinir ağı modelini kullanacağınız probleme göre değişkenlik gösterir. Biz bu problemde Classification ( sınıflandırma ) modelini kullanacağız. Sınıflandırma modellerimizde çıkış katmanında elimizdeki sınıflar kadar nöron vardır ve çıkış katmanındaki her bir nöron bir sınıfı temsil etmektedir. İleri besleme algoritması sonunda çıkış katmanındaki nöronlar arasında en yüksek değeri taşıyan nöronun temsil ettiği sınıf, modelimizin tahminidir.
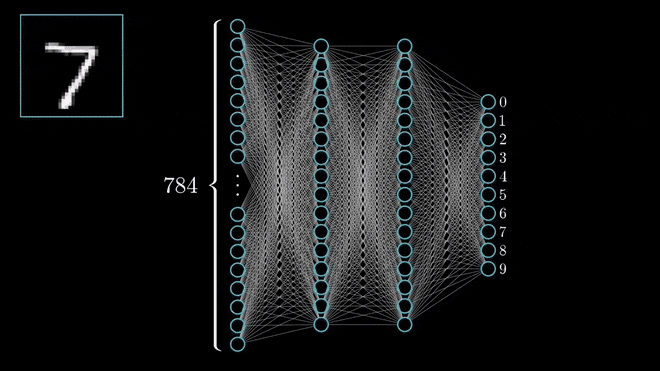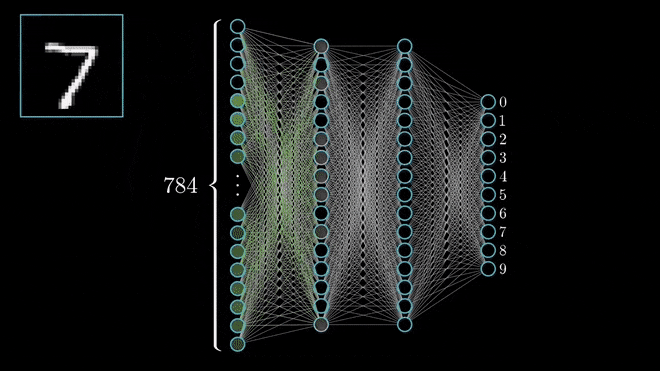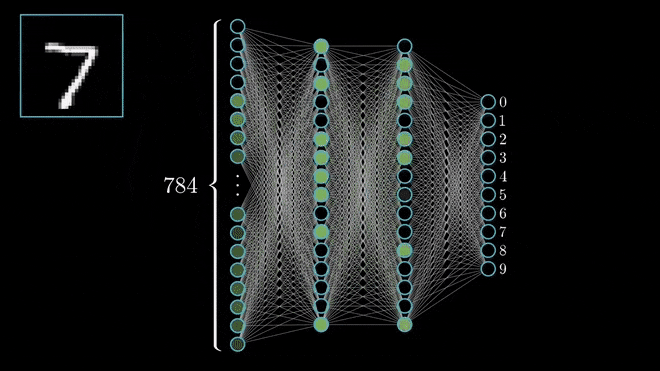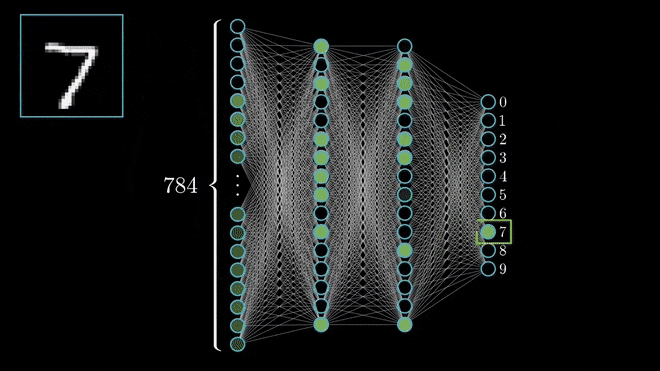
Örnek bir sınıflandırma modeli.
Modelimize öğretmek istediğimiz oyunda oyuncunun 3 kabiliyet hakkı var;
Bu yüzden modelimizin çıkış katmanında 3 nöron bulunduracağız.

Modelimizin çıkış katmanı.
Yukarıdaki fotoğrafta çıkış nöronları arasında 'Sol' sınıfını temsil eden nöron en yüksek z değerine sahip olduğu için modelimiz oyunda 'Sol Oynama' kabiliyetini kullanacaktır.
Şimdilik modelimiz İleri Besleme algoritması ile hangi kabiliyeti oynaması gerektiğini seçebiliyor.
Ancak şuanda hiç bir şey bilmiyor ve tamamen rastgele oynuyor. Çünkü modelimizi eğitmedik.
Geriye Besleme algoritması burada devreye giriyor. Modelimizi eğitmek için Geriye Besleme
algoritmasını inceleyelim;
Geriye besleme algoritmasında yapmaya çalıştığımız şey, modelimizin verdiği kararlar ile vermesi
gereken kararlar arasındaki hatayı modele yaymaktır. Bunun için bu işlemleri sayısal verilerle ifade
etmemiz gerekiyor.
Elimizde bir veri seti var;
Bu durumda y değerlerimiz sayısal veri değil ancak bizim sayısal verilere ihtiyacımız var.
Örnek bir veri:
Bu örnekte oynanması gereken kabiliyet veri setine göre 'Sağ Oynama' kabiliyeti, bu yüzden geriye
besleme algoritmasında 'Sağ Oynama' kabiliyetini temsil eden nöronumuzu buna benzer girdilerde 1'e
yaklaştırmak, diğer iki nöronumuzu 0'a yaklaştırmak istiyoruz.
Geriye Besleme algoritmasının ilk aşamasında çıkış katmanında nöronların delta değerleri bulunur;
delta: sigmoid_derivative(z) * (z - y);
Çıkış katmanındaki nöronların deltalarını bulduktan sonra, gizli katmanlardaki nöronların deltalarını bulabiliriz. Her bir nöronun deltasını bulmadan önce, error değerini bulmamız gerekir, error değeri, nöronun bulunduğu katmandan bir sonraki katmanda bulunan bütün nöronların deltaları ile, nöronumuz arasındaki ağırlığın çarpımlarının toplamı ile bulunur.
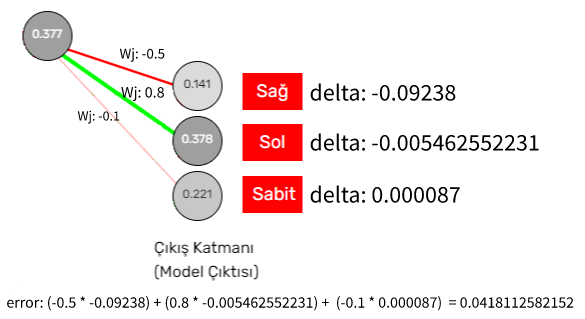
Bir nöronun error değeri hesaplanması.
Bir sonraki adım error değeri hesaplanan nöronun delta değerini bulmaktır. Delta değeri, nöronun error değeri ile z değerinin sigmoid fonksiyonunun türevine tabi tutulmuş haliyle çarpılmasıyla bulunur.

Ara katmandaki bir nöronun delta değeri hesaplanması.
Ara katmandaki nöronların delta değerlerini hesapladıktan sonra sıra deltalara bağlı
olarak nöronlar arasındaki
ağırlıkları güncellemede, bu işleme sondan ikinci katmandan başlıyoruz.
Bir nöron ile kendisinden sonraki katmanda bulunan bir nöronun arasındaki güncel ağırlık, seçili
nöronun z değeri ile sonraki katmanda bulunan nöronun deltasının çarpımının, learning_rate ( genelde
0.6 ) hyperparametresiyle çarpımıyla bulunur.

Ara katmandaki bir nöronun bir sonraki katmandaki herhangi bir nöron ile arasındaki ağırlığın güncellenmesi
Bu işlemi bütün ağ boyunca yaptığınızda veri setini bir kere epoch etmiş olursunuz, ancak modelimizin daha doğru sonuçlar verebilmesi için birçok kez epoch edilmesi gerekir. Bu yüzden başta kötü sonuçlar veren ama zamanla iyileşen sonuçlar ortaya koyan bir model oluşur.

Herşeyi birleştirince ortaya çıkan modelimiz :)
Aktivasyon fonksiyonları, modeimizin çıktılarını linear ( doğrusal ) halden non-linear ( doğrusal olmayan ) hale getirir.
Bu sayede sinir ağın non-linear problemleri de anlayabilecek hale gelir. Bu sayede gerçek dünya problemlerini çözebilme kapasitesine sahip olur.
Bir diğer neden ise çıktıyı türevleyebilmek için türevlenebilen bir fonksiyon içerisine almamız gerekmektedir. Sonuçta öğrenme olarak bahsettiğimiz olay,
sinir ağındaki parametrelerin, hatayı minimize edecek şekilde güncellenmesidir. Bir "y" değerinin "x" değerine göre en yüksek ve en düşük olduğu noktaları bulabilmemizi sağlayan şey türevdir.
Yapay sinir ağlarında da bu amaç ile kullanılmaktadır.
Ayrıca aktivasyon fonksiyonlarının diğer iki özelliği ise, modelimizin çıktılarını sıkıştırmak veya modeli seyrekleştirmektir.
Örneğin sigmoid ve tanh fonksiyonları, modelimizin çıktılarını sıkıştırırken, ReLU ve Leaky ReLU fonksiyonları modelimizi seyrekleştirir.
Relu fonksiyonları negatif değerleri 0'a eşitlerken,Leaky Relu fonksiyonu negatif değerleri 0'ya yaklaştırır. Bu sayede pozitif değerlerimiz daha baskın hale gelir.
Deltalar temel olarak çıkış katmanında hesaplanan hatanın ağın geri kalanına yayılmasında rol alıyorlar.
Bir nöronun ağırlıklarını güncelledikten sonra kendinden bir önceki katmandaki norönların ağırlıklarını güncelleyebilmek için bu nörona ulaşmış hatayı deltalar
aracılığı ile önceik katmandaki nöronlara ulaştırabiliyoruz. Bu sayede çıkış katmanından alınan hata deltalar aracılığı ile ağın geri kalanına yayılmış oluyor.
Kısacası deltalar hatayı taşıyıcı görevini görüyorlar.
Bir türev probleminde problemin minimum noktasına ulaşmak için formülün türevini bir kez almamız yeterli oluyor, bunun nedeni bu problemlerin analitik çözümlerinin olmasıdır.
Örneğin bir bahçenin duvarlarını en az maliyetle kaplayabileceğimiz ve farklı sizelarda karelerin maliyetlerini bildiğimiz bir problemde, bu problemi çözmek için bir kez türev almak yeterli olacaktır.
Çünki bu problem analitik çözüme sahiptir. Bu problemde bahçemizin alanını analitik bir formül ile ( geometrik şekillerin alan formülleri ) bulabiliriz. Ancak
yapay sinir ağlarında problemimizin analitik bir çözümü yoktur. Bu yüzden ağırlıklarımızı güncellemek için bir çok kez epoch etmemiz gerekmektedir.
Zaten amacımız analitik olarak formülize edemediğimiz problemleri çözmek olduğu için bu durumda epoch etmek zorundayız.
Learning rate değerimiz, ağırlıkların ne hızda güncelleneceğini belirler. Bu hız binevi bir adım büyüklüğüdür. Eğer adımımız çok büyük ( learning değeri çok yüksek ) olursa
minimum hata noktasını atlayabiliriz. Aynı şekilde adımımız çok küçük olursa minimum hata değerine ulaşmamız daha fazla zaman alır veya ulaşmamız mümkün olmayan sürelere çıkabilir.
Tabiki de başlangıçta adımlarımızı büyük tutup daha sonrasın küçültebiliriz. Bu yönteme de learning rate decay ( öğrenme hızı azalması ) denir ve bu yöntemde learning rate her bir kaç epochta bir azalmaktadır.
Eğer ağımızdaki her bir nöron aynı değer ile başlamış olsaydı ağımızın ağırlıkları geniş bir uzaya yayılamaz ve ağımızın genelleme yeteneği kısıtlı kalırdı. Yani daha fazla epoch gerektirirdi ki bazı durumlarda daha fazla epoch da çözüm olmayabilirdi.
Bir diğer bakış açısıyla eğer nöronlarımızı simetrik, veya bir formüle dayalı olarak başlatsaydık, yine aynı durumla karşılaşırdık. Ağımızın ağırlıkları geniş bir uzaya yayılamaz ve o formülün etrafında sıkışıp kalırdı.
Bu yüzden ağırlıklarımızı rastgele başlatıyoruz ki ağımızın parametreleri daha geniş bir uzaya yayılsın ve ağımızın genelleme yeteneği artmış olsun.
Evet modelimizi istediğimiz kadar büyütebiliriz. Ancak bu durumda daha büyük işlem kapasitesine sahip cihazlar gerekmektedir.
Örneğin ben bu modelde hem oyunu öğrenebilecek kadar büyük hem de mobil cihazların işlem kapasitesinde de çalışabilicek kadar küçük seçmeye, yani bir denge kurmaya çalıştım.
Tabiki tek sorun bu değil, daha büyük modeller küçük problemlerde daha fazla overfitting ( aşırı öğrenme, ezberleme ) yapabilirler. Overfitting durumu modelin kendisine verilen verisetini ezberlemesi ve genelleme yapma yeteneğinin körelmesi anlamına gelmektedir.
Ayrıca büyük modeller daha fazla veri ile eğitilmelidirler.
Bu yüzden modelimizin sizeunu problemin büyüklüğüne ve karmaşıklığına göre seçmeliyiz.
Sigmoid fonksiyonu ve türevinin tanımlanması ve gerekli random fonksiyonları
function random(min, max) {
return Math.floor(Math.random() * (max - min)) + min;
}
function random_f(min, max) {
let df = 0;
while (df == 0) {
df = random(min, max) * Math.random();
}
return df;
}
function sigmoid(x) {
return 1 / (1 + Math.exp(-x));
}
function sigmoid_derivative(y) {
return y * (1.0 - y);
}
Katman sınıfının oluşturulması
class Layer {
constructor(size) {
this.z_ = Array(size);
this.delta_ = Array(size)
this.biases = [];
this.weights = [];
for (let i = 0; i < size; i++)
this.biases.push(random_f(-4, 4));
}
}
Modelin oluşturulması
class model_DL {
constructor(layer_sizes, learning_rate = 0.6, labels, first_weights = 0) {
this.Layers = [];
this.layer_sizes = layer_sizes;
this.weights = {};
this.learning_rate = learning_rate;
this.labels = labels;
this.Layers.push(new Layer(layer_sizes[0]));
for (let i = 1 ; i < layer_sizes.length;i++) {
let size = layer_sizes[i];
let layer = new Layer(size);
for (let j = 0; j < size; j++) {
let w_ = [];
for (let p = 0; p < layer_sizes[i-1]; p++){
w_.push(random_f(-4, 4));
}
layer.weights.push(w_);
}
this.Layers.push(layer);
}
let ind = 0;
if (first_weights != 0) {
for (let p of this.Layers) {
for (let a = 0; a < p.weights.length; a++) {
for (let i = 0; i < p.weights[a].length; i++) {
p.weights[a][i] = first_weights[ind];
ind++;
}
}
}
}
}
}
var model_hidden_layer_sizes = [2, 12, 10, 8, 3];
var model = new model_DL(layer_sizes = model_hidden_layer_sizes,
learning_rate = 6e-1,
labels = ["sag", "sol", "sabit"]);
İleri besleme algoritmasının tanımlanması
get_activ(x_data, weights, b) {
let g = x_data.map(function (x, index) {
return weights[index] * x
})
let sum_ = g.reduce((sum_, x) => sum_ + x) + b
return sigmoid(sum_);
}
set_data(x) {
this.katmanlar[0].z_ = x.concat();
let i = 0;
while (i < this.katmanlar.length - 1) {
let katman = this.katmanlar[i];
let skatman = this.katmanlar[i + 1];
let p = 0;
while (p < skatman.z_.length) {
this.katmanlar[i + 1].z_[p] = this.get_activ(katman.z_,
skatman.weights[p], skatman.bler[p]);
p++
}
i++
}
}
Predict (tahmin) fonksiyonunun tanımlanması
output_layer() {
return this.Layers[this.Layers.length - 1];
}
predict(x) {
this.set_data(x);
return this.labels[this.output_layer().z_.indexOf(Math.max(...this.output_layer().z_))];
}
Geriye besleme algoritmasının tanımlanması
epoch(x_data, y_data) {
let index = 0;
while (index < x_data.length) {
let x = x_data[index];
let y = y_data[index];
this.predict(x);
let i = 0;
while (i < this.output_layer().z_.length) {
let h = this.output_layer().z_[i];
let y_actual = y == this.labels[i] ? 1 : 0;
let delta = sigmoid_derivative(h) * (h - y_actual);
this.Layers[this.Layers.length - 1].delta_[i] = delta;
i++;
}
let g = this.Layers.length - 2;
while (g > -1) {
let delta_ = this.Layers[g + 1].delta_;
let after_layer = this.Layers[g + 1];
let layer_ = this.Layers[g];
this.Layers[g].delta_ = this.Layers[g].z_.map(function (x1, index1) {
return after_layer.weights.map(function (x, index) { return x[index1] * delta_[index] }).reduce((sum_, x) => sum_ + x) * sigmoid_derivative(layer_.z_[index1]);
});
g--;
}
i = 1;
while (i < this.Layers.length) {
let delta_ = this.Layers[i].delta_;
let learning_rate = this.learning_rate;
let Layers = this.Layers;
let gradients = delta_.map(function (x, index) {
return Layers[i - 1].z_.map(function (x1, index) {
return x * x1 * learning_rate;
});
});
this.Layers[i].weights = this.Layers[i].weights.map(function (x, index1) {
return x.map(function (x, index) {
return x - gradients[index1][index];
});
}).concat();
this.Layers[i].biases = this.Layers[i].biases.map(function (x, index) { return x - (delta_[index] * learning_rate) })
i++;
}
index++
}
}